2013年元月调考复习—正多边形与圆试题及答案
试题简介:武汉中考网12月11日:2013元月调考数学考点范围抓好圆内证明计算(难点)、圆与坐标系数形结合(难点)、旋转与全等常见模型(难点)、旋转与分类讨论多解性(难点)、一元二次方程与根式(重点)、概率树形图(重
试题类型:数学练习题 > 2013年元月调考复习—正多边形与圆试题及答案
元月调考复习—正多边形与圆
(一)正多边形与圆
1、问题背景,某课外学习小组在一次学习研讨中,得到如下两个命题;
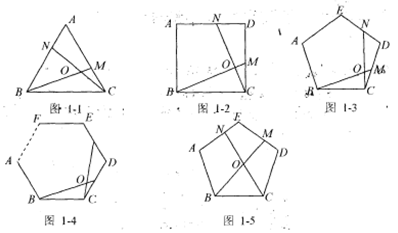
①如图1-1,在正三角形ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若BON=60°,则BM=CN。
②如图1-2,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
③如图1-3,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=180°,则BM=CN。
任务要求:
(1)请你从①②③三个命题中选择一个进行证明。
(2)请你继续完成下面探索:
①如图1-4,在正n(n≥3)边行ABCDEF…中,M、N分别是CD、DF上的点,BM与CN相交于点O,问当BON等于多少度时,结论BM=CN成立?
②如图1-5,在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,当∠BON=108°时请问BM=CN是否成立,并说明。
2.探究:某班在探讨正多边形问题时,得到以下命题:
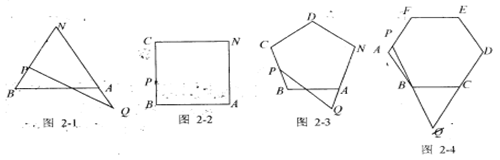
①如图2-1,正△ABN,P、Q分别从B、A出发,在边BC及NA的延长线上运动,若BP=AQ,则M是PQ的中点。
②如图2-3,正五边形BCDN,P、Q分别从B、A出发,在边BC、NA的延长线运动,若BP=AQ,则M是PQ的中点。
归纳:对于正多边形ABC…N,P、Q分别从B、A出发,在边BC、NA的延长线上运动,若BP=AQ,则M为PQ的中点。
(1)请你从两个命题中任选一个进行证明。
(2)请在图2-2中根据上面归纳画出图形,并比较AM和BM的大小:AMBM。
(3)如图2-4,正六边形ABCDEF中,P在边CD上,PB交NA的延长线于Q,求证:BP=BQ.
|
请下载附件: |
|
《2013年元月调考复习—正多边形与圆试题及答案.word》 |
 相关阅读:
相关阅读:



